Versus és una preposició, sovint abreujada com vs., que indicava en llatí direccionalitat (la podem traduir com cap a o en direcció a, ja que la paraula que en deriva en català, vers, està restringida , cada vegada més, a contextos literaris). Versus va donar la preposició vers (idèntica en català i en francès) o verso en italià. Ja en el segle XV però, els anglesos la introdueixen en el seu llenguatge jurídic amb el significat de contra i així, més tard passa al llenguatge, sobretot esportiu, denotant combat o enfrontament més o menys incruent (Muhammad Ali vs. George Foreman o Argentina vs. Uruguai) i així ens va arribar a nosaltres, primer del castellà i sobretot a través de la premsa esportiva. Podia haver escrit en el títol: l'arrel de dos contra el nombre auri, però com que —misteris de la ment en vacances— m'ha vingut al cap el film Dracula vs. Frankenstein (1971) del director Al Adamson he optat per versus. Per als professors, les proporcions, √2 i Φ (el nombre auri) no són equiparables als monstres; però per alguns alumnes, potser sí. Els aficionats a les pel·lícules de sèrie B, aquelles de tarda i vespre de sessió doble, em poden recordar que el director espanyol Jesús Franco també va rodar una infame Drácula contra Frankenstein (1974) amb el contra al títol..., però ja és hora que acabem aquesta digressió.
Per introduir aquest tema ho farem amb un qüestió del nivell 3 (1r de batxillerat) de la prova Cangur de l'any 2005 (feu clic damunt de l'enunciat per poder-lo llegir amb més comoditat):
No és massa complicat de trobar la resposta, intenteu-ho i si desistiu consulteu l'enllaç DIN 476 on trobareu la solució i informació sobre la norma DIN 476 que és la que regula els formats dels fulls que generalment utilitzem. Haureu llegit en l'enllaç anterior que les regles per fixar-ne les dimensions són molt senzilles:
- Tots els fulls de la sèrie DIN tenen la mateixa proporció entre el seu costat gran i el seu costat petit.
- Dues grandàries de paper successives han de complir que l'àrea d'una ha de ser el doble de l'altra. Com hem vist en el problema, per exemple, ajuntant dos fulls DIN A4, tenim un full DIN A3.
- Un full DIN A0 té una àrea d'un metre quadrat.
29,7 ÷ 21,0 = 1,41428571428571428571428571428571...
Obtenim un decimal periòdic mixt amb un 4 com a primer decimal i un perìode de sis dígits, 142857, que es va repetint (en forma fraccionària aquest nombre és 99/70). Si comparem aquest nombre amb l'arrel de dos (√2 = 1,414213562373095048801688724209...), veiem que coincideixen en els primers quatre decimals. Recordem que quan vam intentar comprovar si les targetes de crèdit eren rectangles auris (El mite del nombre d'or) ja ens fallava el primer decimal. Abans de proclamar vencedora a √2 enfront de, o versus, Φ, almenys si analitzem la seva presència en formats nomalitzats, podem presentar alguna objecció. No és massa correcte comparar un full DIN A4 amb una targeta de crèdit, cal cercar el format DIN que més s'hi aproxima en magnitud. Aquest és el DIN A8 (52 mm x 74 mm), però si voleu podem provar també amb el DIN A7 (74 mm x 105 mm) (veieu Mida de paper).
DIN A8: 74 ÷ 52 = 1,4230769230769230769230769...
DIN A7: 105 ÷ 74 = 1,4189189189189189189189189...
Tal com era d'esperar, l'aproximació no és tan bona, però continua sent remarcable.
Per què els llibres de text i les pàgines web continuen insitint amb els rectangles auris quan parlen de proporcionalitat? √2 permet parlar amb rigor, dóna joc a parlar de formats de paper i de fotografia, d'ampliacions i reduccions..., però no té la poesia mítica de Φ!
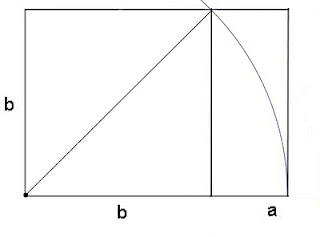
Construcció d'un rectangle amb raó de proporcionalitat √2
Com que ja vam explicar com dibuixar un rectangle auri en l'entrada anterior a aquesta (Com dibuixar rectangles auris), no seria just que no parléssim de com representar gràficament els rectangles que compleixen que costat major ÷costat menor = √2. El mètode és semblant i molt més senzill en aquest cas.
Cap comentari:
Publica un comentari a l'entrada